Stephanie Dodson

Stephanie Dodson

Assistant Professor, Mathematics Department, Colby College

Research

Patterns are ubiquitous in biological and physical processes. The propagation of electrical pulses in cardiac tissue, oscillations of chemical reagents, and movement of animals are all examples of naturally occurring spatiotemporal patterns. I am an applied mathematician who is motivated by how math can be used to uncover the fundamental principles of the natural world. I have studied the formation and stability of spatiotemporal patterns related to cardiac arrhythmia, chemical oscillations, and blue whale migrations. Summaries of recent and ongoing projects are below.

Traveling Waves and Cardiac Arrhythmia

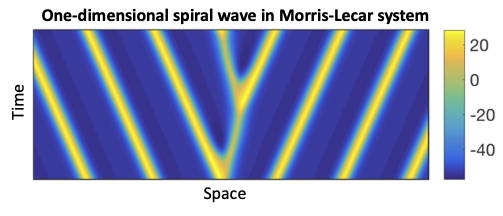
Regular cardiac function is characterized by coherent, periodic traveling waves of electrical activity driving heartbeats. When this process goes awry, the ensuing abnormal and irregular rhythms are known as arrhythmias. Much of my research has focused on studying traveling waves and patterns that contribute to arrhythmia initiation and termination.

Throughout this area of research, I focus on spiral and traveling waves waves that arise in reaction-diffusion systems, and I apply a variety of analytical and computation techniques motivated by methods in dynamical systems and nonlinear waves.



Pattern Formation

changing pattern

Spatially periodic patterns are observed in a multitude of applications and importantly, the existence and stability of these patterns can have profound consequences for the system. For example, the arrangement into spatial patterns has been shown to be a productive strategy that can delay the extinction of vegetation and other populations experiencing harsh conditions. A core ingredient necessary for patterns to arise is the existence of processes that promote activation and inhibition over multiple spatial scales. We study a reaction diffusion model for a population that contains nonlocal competition and facilitation terms in order to determine characteristics at pattern onset and the behavior of patterns in parameter regimes far from pattern onset.


Agent-Based Models and Migrations of Blue Whales

Northern Pacific blue whales are a highly dynamic population that make vast yearly migrations to meet their energetic needs. Along with collaborators, we developed and analyzed agent-based models to investigate how environmental and prey conditions and social calls impact the migratory behavior. The model accurately captures migration behaviors and yearly differences in the spatiotemporal distribution driven by variations in prey abundance.